Day 48: What Happened When I Gave Them the Answers
[TL;DR – Not as much as I had hoped.]
College-Prep Physics: Students came to class with the following question completed for homework:
You are on a sleigh ride in Central Park one brisk winter evening. The mass of the sleigh with everyone in it is 250 kg, and the horses are pulling the sled with a combined horizontal force of 500 N. The sled moves at a constant speed of 3.33 m/s.
(a) What is the force of kinetic friction on the sleigh?
(b) What is the coefficient of kinetic friction between the sleigh and the ground?
I asked everyone to whiteboard their answers. I heard some students say they didn’t get it. Several other students came up to me — worksheet in hand — to ask if their answer was right.
“I’m going to give you the answers,” I said. “Here they are.”
“Now on your whiteboards, I want you to explain why those are the answers.”
If you think about it, the answers to those questions are pretty simple. But the detailed explanations about how to get those answers aren’t simple and require several steps of reasoning. In the past, I’ve told my students that I could care less about the answers. I want to see their reasoning instead. And today I finally owned up to that.
And here’s what they said for part (a):
Only the last one comes close to a full explanation, in my opinion. Here’s the complete chain of reasoning:
- The sleigh is moving at a constant speed, which means that the forces on the sleigh must be balanced.
- Looking at a force diagram for the sleigh, we see that, in the horizontal direction, the horses pull forward and friction pulls backward.
- In order for those two forces to be balanced, they must be equal in size.
- Therefore, if the horses pull 500 N forward, then the friction force must be 500 N backward.
That is a lot of steps which, in the end, yield an answer that’s a number already given in the problem statement.
We rarely write down those steps when we work a problem at the board or have kids whiteboard their work. Now think about a kid who goes to look back at their worksheet to study for an upcoming quiz. What’s typically going to be on that kid’s worksheet?
500 N. The answer. That’s all. Because we unintentionally send the message that the answer is all that matters. Even when we say the answer doesn’t matter, the assignments we give kids typically don’t make good on that statement.
Now how about part (b)?
Many groups used the friction formula correctly, but their work is still far from being an explanation as to why the answer is 0.2. The complete chain of reasoning is:
- The sleigh is moving at a constant speed, which means that the forces on the sleigh must be balanced.
- Looking at a force diagram for the sleigh, we see that, in the vertical direction, the gravitational force from the earth pulls downward and the normal force from the ground pushes upward.
- In order for those two forces to be balanced, they must be equal in size.
- Therefore: Fn = Fg = m*(9.8 N/kg) = (250 kg)*(9.8 N/kg) = 2450 N
- The coefficient of friction is the ratio of the friction force to the normal force.
- Therefore: coefficient of friction = Ff/Fn = 500 N / 2450 N = 0.2 N/N.
Again, relatively simple math, but complex reasoning. Do kids realize that when they just “multiply kilograms by 9.8” they’re actually finding the gravitational force, not the normal force? Why is the normal force the same value in this case?
I know that some of this reasoning comes out verbally during whiteboard sharing and questioning (within groups and between groups). But how much of that reasoning gets written down so it can be referred to later? Or simply writing it down as a way to make the students’ own thoughts clearer or to self-identify holes in their own understanding?
[Coincidentally related: Michael Pershan’s post today — Is Your Own Math Work Shareable?]
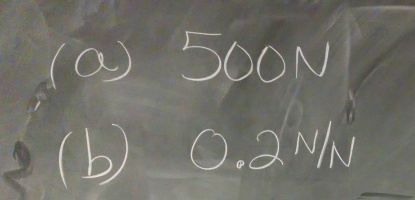



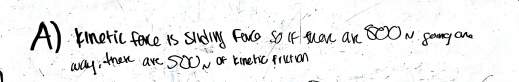

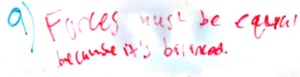

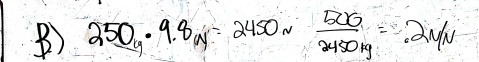
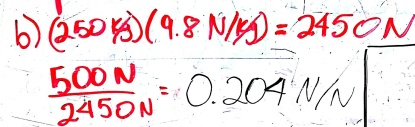


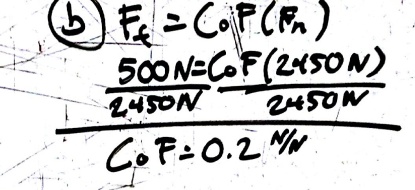
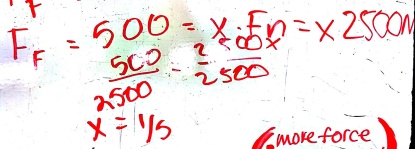
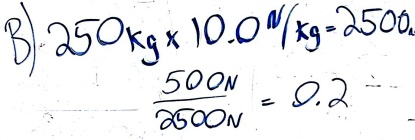

This reminds me that I have been tempted to try and construct questions on assessments where the final answer is not actually worth any of the points to be earned. Haven’t been brave enough to take that step.
In my first year of teaching, I would give the correct answers on all of my physics tests on each question. My college professors did this for any questions where a correct answer was needed to move forward on another part of the question. I found that my students were not mature enough to manage their time on tests like that. Clearly my focus was on the work/demonstration of thinking and not the answer, but the students would not move on knowing that they had not arrived at the correct solution. It caused major anxiety and I quickly ended the practice.
Interesting post- I just gave back a worksheet on projectile motion with the hoops, where most of the class did rather poorly because they did not clearly show their work- how they got from one step to the next. I did allow them to redo it so they get in the habit of expressing themselves clearly. Not only do they need to understand what their line of thinking was, but they need to learn to express themselves clearly to others also.
This is a great inspiration a solid strategy to improve the communication of the processes that students go through with their problem solving. I’ve been using apps like Educreations and Show Me to allow learners to record their thinking on problems, but they tend to simply use words to tell the math. By forcing them to think backwards and analyze this on a regular basis could change the way they express themselves. I will let you know how my experiments go over the next few units.
My colleagues and I are going to try having the students write proofs of problems next year. I envision something similar to your listed reasoning steps above.
We don’t have the plan solidified but so far we plan to give groups of students different problems (with the answer) and have them do the following: 1) at least 3 representations of the problem (diagram, graphs, FBD, etc), 2) assumptions if needed, 3) “pre-math” knowledge (I can’t think of another name for it), 4) each mathematical step, and 5) reasons for each mathematical step. We’re thinking a T-chart would help organize it for the kids.
I’m not sure #5 is that important for our AP students who are pretty solid with their math but we think it might help the kids in regular physics. Those statements might be something like “multiply both sides of the equation by 2 to move the 1/2 from the right side to the left side of the equal sign”.
The “pre-math” knowledge would be like “constant velocity, so forces are balanced” sort of statements like the first few you have listed above. If you can think of a better name for it please let me know.
We have a strict district calendar to follow so we don’t have as much time for discussion as we really need. I’m not sure we’ll be able to whiteboard all of these problems… but hopefully at least some!
Thanks for the awesome blog, too! I love reading it!
I also try this on a regular basis. I give students the answers to the questions and ask for the explanation of how.. It’s amazing at the blank stares. I am now using the same process with GoogleClassroom. Students work in groups and come up with answers / steps without regard for the answer. This seems to work well for me.